Accuracy in intraocular lens (IOL) calculations and postoperative outcomes has taken on another level with the availability of toric IOLs. The ability to correct corneal astigmatism at the time of cataract surgery reduces the need for spectacles postoperatively making the necessity to calculate the optimal power of the IOL ever more important.
Calculating an accurate toric intraocular lens power
Knowing and understanding what parameters and adjustments are incorporated both in the biometry and the toric calculator used to calculate an accurate toric IOL power is a major advance to improving outcomes.
The spherical component of the IOL is calculated by the biometry device using personalised constants in various IOL formulae based on analyses of previous cases. The instrument of choice uses the resulting effective lens position (ELP) from modern third (Holladay 1, Hoffer Q, SRK/T) and fourth generation (Holladay 2 and Haigis) formulae to determine the power of the IOL. The third generation formulae utilise corneal power and axial length to predict the ELP whilst the fourth generation formulae address the relationship between anterior chamber depth (ACD) and the length of the posterior segment and as a result have a higher rate of accuracy over a wider range of axial lengths. The fifth generation formulae (Olsen and Barrett Universal II) can provide even better accuracy incorporating ray tracing and lens thickness.
Most of today’s theoretical IOL formulae will give very good outcomes for the average eye where the axial length is between 22 mm and 24 mm and the corneal power centrally in the range of 42.00−45.00 D. However, what do we need to factor in outside these ranges?
1. For axial lengths above 25.00 mm as described by Wang and Koch:1
Holladay 1
Optimised AL = 0.8814 x IOL Master AL + 2.8701
Haigis
Optimised AL = 0.9621 x IOL Master AL + 0.6763
SRK/T
Optimised AL = 0.8981 x IOL Master AL + 2.5637
Hoffer Q
Optimised AL = 0.8776 x IOL Master AL + 2.9269
AL = axial length
Without these adjustments an unexpected amount of hyperopia occurs.
2. For eyes with an axial length less than 22.00 mm the Hoffer Q and Holladay 2 work well.
3. For long eyes consider using the SRK/T or Barrett formulae.
It is important to remember that a 100 micron inaccuracy in the axial length translates to a 0.28 D error in the refraction. Furthermore, a calibrated keratometer assigned to biometry measurements as a cross-check to the keratometry readings from the biometer will play a major role in optimising refractive outcomes.
The ELP will also impact the final refraction – a lens that sits further back than expected will lead to postoperative hyperopia while a lens that sits further forward than expected will result in myopia. Hence, knowing which IOL formula to use is most important.
Detecting inconsistent measurements during biometry
1. A difference in 1.00 D in IOL power between right and left eye should be confirmed.
2. A significant difference between axial length or keratometry between eyes.
The same is true of toric IOL calculators where different amounts of toricity can be calculated depending on what adjustments have been allowed for.
What to look for in your toric intraocular lens calculator
1. The conversion of the IOL power from the IOL plane to the corneal plane should be based on the ELP and not fixed. The toricity of the IOL at the corneal plane will also vary depending on the power of the spherical component of the IOL so that a +33 D sphere will have a different effect on the toricity compared with a +15 D sphere. It is therefore important that the calculator incorporates the sphere when converting the power of the toric IOL.
2. The Spherical Equivalent power calculated together with the toricity and not simply adding on the toricity to the spherical equivalent calculated by the biometry device. This can then calculate and display the expected sphero-cylindrical refraction and not just the cylinder magnitude and axis.
3. The axial length inclusion is paramount in determining an accurate IOL power; a 1 mm change in axial length can change the IOL power by 2.5 D. An average or fixed axial length should not be used.
4. Allowance for inclusion of personalised IOL constant: A constant, Surgeon Factor, pseudophakic anterior chamber depth (pACD), Haigis a0, a1, a2. These are important for optimising visual outcomes.
5. Use measured total corneal power from tomographer instead of nomograms when available as there is a widespread contribution of the posterior corneal astigmatism to the total corneal astigmatism, particularly for against-the-rule corneal astigmatism where there is considerable variability in the meridian of the posterior corneal astigmatism, which affects its effective magnitude, and therefore nomograms are only an estimate.2 Caution should be used when applying nomograms such as the Baylor nomogram3 to the anterior corneal power measurement to ensure that the toric calculator is not already factoring in an adjustment for this.
6. Be aware if the toric IOL calculator you are using is already factoring in the total corneal power so by inputting the parameters of total corneal power you are double up on the contribution of the posterior cornea. The total corneal astigmatism can be calculated on many of the tomographers available including the Pentacam (OCULUS, Wetzlar, Germany), the Sirius (CSO, Firenze, Italy) and the Galilei (Ziemer, Port, Switzerland), which would indicate a more accurate measure than relying on nomogram adjustment of the anterior corneal astigmatism to determine the contribution of the posterior cornea. The corneal topographic astigmatism (CorT) total parameter as a measure of total corneal astigmatism has been shown to be more accurate than anterior corneal measures such as CorT anterior, simulated keratometry, manual keratometry and corneal wavefront.4,5
7. Note that anterior corneal astigmatism should still be used for calculation of the spherical component of the IOL using 3rd and 4th generation formulae. So the toric IOL calculator should have two entry fields for corneal astigmatism if it is also calculating the spherical component of the IOL, one for anterior corneal astigmatism and one for total corneal astigmatism.
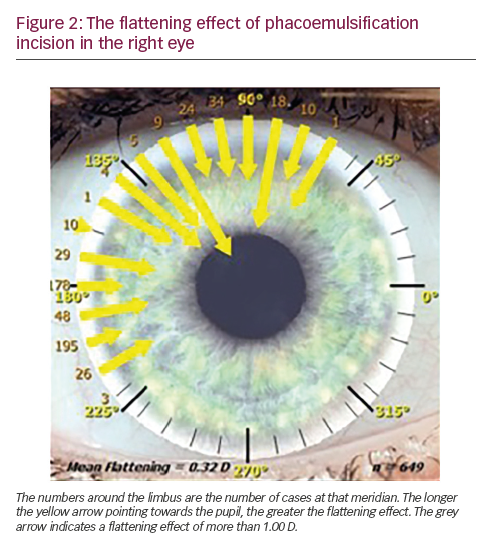
8. The flattening effect (FE) of the phaco (main) incision calculated from previous analyses as this can change the magnitude and/or orientation of the corneal astigmatism that is being neutralised by the toric IOL. The surgically induced astigmatism vector (SIA) is an overestimation of the incisional effect as this is composed of both the flattening effect and the rotational effect known as the torque (Figure 1). It is important to note that the SIA increases with increased corneal
astigmatism so the SIA or FE is not constant; for a 1 D increase in astigmatism the SIA increases by 0.37 D.6 The SIA also varies on whether the incision is placed on the steep or flat meridian.7
Retrospective analyses of phaco incisions separately for each eye can determine the amount of flattening at specific corneal meridia (Figure 2). This can then be used for future procedures to more accurately determine the effect of the incision on the corneal astigmatism (magnitude and orientation) before calculating the required toricity of the IOL.
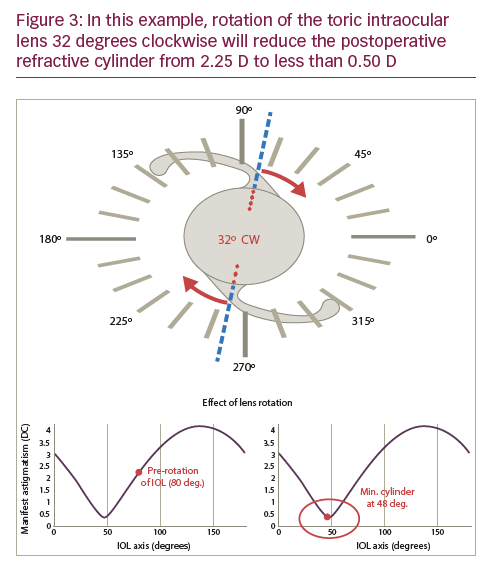
9. Does the toric IOL calculator have the ability to analyse and calculate any required rotation of the toric IOL to minimise the refractive cylinder postoperatively should there be a refractive cylinder surprise (ASSORT Toric IOL Calculator, www.assort.com)? This new axis may not necessarily coincide with the postoperative steep corneal meridian.
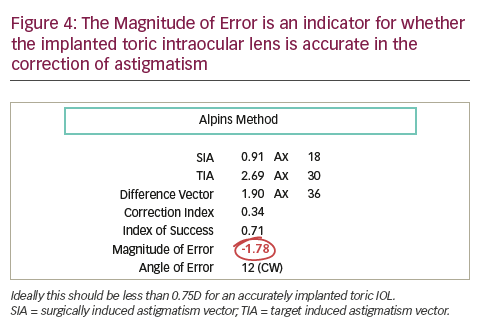
The example shown in Figure 3 shows a refractive cylinder surprise of -2.25 D x 105. Rotation of the toric IOL 32 degrees clockwise reduces the refractive cylinder to less than 0.50 D. The alignment of the toric IOL may be exactly where it was intended to be and yet there is still a refractive cylinder surprise; this may be attributed to non-lens ORA8 which is pre-existing and originating from retinal tilt and/or cortical perception. Futhermore, does the calculator indicate whether the correct toricity of the IOL has been implanted to avoid IOL exchange and opt for the possibility of laser-assisted in situ keratomileusis (LASIK) instead. The Alpins Method of astigmatism analysis9 for toric IOLs calculates the Magnitude of Error (ME) which indicates whether the toricity of the implanted IOL is too strong or too weak with 0.00 D being the ideal. The example in Figure 4 shows an ME of -1.78 D indicating that the implanted IOL is more than 1.50 D under powered. Should the ME indicate less than 0.75 D then LASIK would be the remaining option without exchanging the IOL.
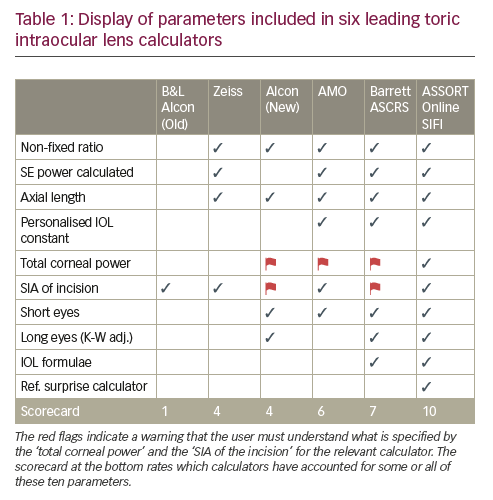
Understanding and interpreting what the biometry and the toric IOL calculator use and allow for in the calculation of the IOL is imperative to obtaining optimal visual outcomes postoperatively. With many toric IOL calculators now available online, the objective should be to use the check list discussed in this article and select one that covers these important features (Table 1). Any effective formula needs to be coexisting in a calculator with these features to enable it to perform at its optimal capacity.







